自然数的个数是什么的
自然数的个数是(无数的)。
自然数是指用以计量事物的件数或表示事物次序的数。即用数码0,1,2,3,4……所表示的数。自然数由0开始,一个接一个,组成一个无穷的集体。自然数有有序性,无限性。分为偶数和奇数,合数和质数等。
自然数在日常生活中起了很大的作用,人们广泛使用自然数。自然数是人类历史上最早出现的数,自然数在计数和测量中有着广泛的应用。人们还常常用自然数来给事物标号或排序,如城市的公共汽车路线,门牌号码,邮政编码等。
自然数是整数(自然数包括正整数和零),但整数不全是自然数,例如:-1-2-3......是整数而不是自然数。自然数是无限的。
全体非负整数组成的集合称为非负整数集,即自然数集。
在数物体的时候,数出的1.2.3.4.5.6.7.8.9……叫自然数。自然数有数量、次序两层含义,分为基数、序数。
基本单位:计数单位:个、十、百、千、万、十万......。

自然数的个数都是什么?
自然数个数是无数个。
自然数用来数物体个数的,最小的是0.没有最大的自然数,自然数的的个数是无穷多个。
自然数用以计量事物的件数或表示事物次序的数。即用数码0,1,2,3,4,……所表示的数。表示物体个数的数叫自然数,自然数由0开始,一个接一个,组成一个无穷的集体。自然数有有序性,无限性。分为偶数和奇数,合数和质数等。
性质和特点:
1、有序性。自然数的有序性是指,自然数可以从0开始,不重复也不遗漏地排成一个数列:0,1,2,3,…这个数列叫自然数列。
2、无限性。自然数集是一个无穷集合,自然数列可以无止境地写下去。
3、传递性:设n1,n2,n3都是自然数,若n1>n2,n2>n3,那么n1>n3。
4、三岐性:对于任意两个自然数n1,n2,有且只有下列三种关系之一:n1>n2,n1=n2或n1<n2。
5、最小数原理:自然数集合的任一非空子集中必有最小的数。
自然数集N是指满足以下条件的集合:
①N中有一个元素,记作1。
②N中每一个元素都能在N中找到一个元素作为它的后继者。
③1是0的后继者。
④0不是任何元素的后继者。
⑤不同元素有不同的后继者。
⑥(归纳公理)N的任一子集M,如果1∈M,并且只要x在M中就能推出x的后继者也在M中,那么M=N。
参考资料:
百度百科——自然数
自然数的个数是几?
自然数最小的是0,但没有最大的,所以,自然数的个数是无限个。
自然数的个数是无数个。自然数的个数是无限的.最小的自然数是0,没有最大的自然数.
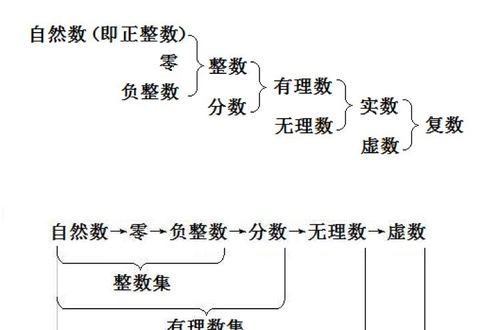
自然数 包括哪些数
自然数表示物体的个数,0表示一个也没有,所以自然数从0开始的整数即:0,1,2,3,……最小的自然数是0z自然数包括0和正整数,最小的自然数是01, 2, 3, 4, 5, ......
最小的自然数是 1 .自然数就是我们常说的正整数和0。
即用数码0,1,2,3,4,……所表示的数 。表示物体个数的数叫自然数,自然数由0开始(包括0), 一个接一个,组成一个无穷的集体。我们在数物体的时侯,用来表示物体个数的1、2、3、……叫做自然数,或叫做正整数。一个物体也没有,用0表示。0也是自然数。
最小的自然数是0,没有最大的自然数,自然数的个数是无限的。
自然数起源于数(shu),是由于计数(shu)物体的需要,经过很长的历史阶段,逐渐产生的。
远古时代,由于人类在最初要分配劳动工具和劳动果实,产生了计数物体的需要。人类在捕鱼、狩猎和采集果实的劳动中,有时有收获,有时没有收获,这样,逐渐形成了“有”和“无”的概念;有时收获够分配,有时收获不够分配,这样,逐渐形成了“多”和“少”的概念。例如,人们出去打猎的时候,要数一数一共出去了多少人,拿了多少件武器;回来的时候,要数一数捕获了多少只野兽等。这样就产生了数。
由于生产的发展,劳动的收获增加了,人们有了计数的需要。起初,人们用实物来计数。例如,用手指或脚趾,用结绳或刻痕,用石子或木棒。计数采用一一对应的方法。例如,为了表示捕获的三只羊,就弯曲三个手指;为了表示捕获的三条鱼,也弯曲三个手指。又经过较长的时间,人们知道把彼此等价的东西归为一类,并在每一类中找出一个“标志”来表示这类物体的共同特征。逐渐地,把表示数量的那些实物的名称如“手指”、“石子”等,脱离它的原始意义,变为单纯的数的名称,自然数就这样产生了。
“1”是自然数的单位。任何一个非0自然数都是由若干个“1”组成的。自然数的个数是无限的,没有最大的自然数。
〔自然数的单位〕
任何一个非0自然数都是由若干个“1”组成的。所以1是自然数的单位。如:8是由8个1组成的,25是由25个1组成的。
参考资料:?forum=62&topic=2020





