这个题怎么求2阶导数
可以用公式求,y''(x)=(y''(t)x'(t)-x''(t)y'(t))/x'³(t)然后分别求出x'(t),y'(t),x''(t)和y''(t)即可(2) (f(x^2))' 链式法则 =f'(x^2) . (x^2)' =f'(x^2) . (2x) =2x.f'(x^2) (f(x^2))'' 2阶导数=1阶导数再求导数 =((f(x^2))')' =(2x.f'(x^2))' 链式法则 =2[ x.【f'(x^2)】' + f'(x^2). (x)']=2[ x f''(x^2).(x^2)' + f'(x^2)] =2[ x f''(x^2).可以用公式求,y''(x)=(y''(t)x'(t)-x''(t)y'(t))/x'³(t)然后分别求出x'(t),y'(t),x''(t)和y''(t)即可

这几题的二阶导数怎么求,求帮忙,谢谢!
(f(x^2))'
=f'(x^2).(x^2)'
=f'(x^2).(2x)
=2x.f'(x^2)
(f(x^2))''
2阶导数=1阶导数再求导数
=((f(x^2))')'
=(2x.f'(x^2))'
=2[x.【f'(x^2)】'+f'(x^2).(x)']
=2[xf''(x^2).(x^2)'+f'(x^2)]
=2[xf''(x^2).(2x)+f'(x^2)]
=2[2x^2.f''(x^2)+f'(x^2)]
二阶导数和二阶偏导数的区别?二阶导数和二阶偏导数的区别
变量个数不同。
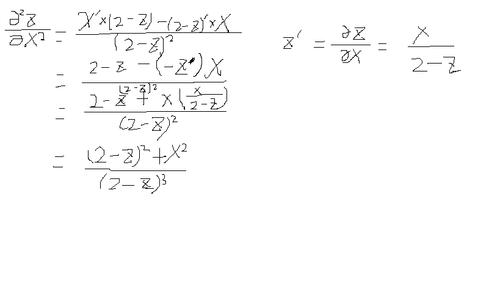
求二阶导数
那要看对谁求导了,如果x,y都是变量,也就是y不是x的函数的话,要对x求导的话,可以吧y^3当做常数,直接对x^3求导即可,求完是6*x。如果y是x的函数,而对x求导,就是
6*x+6*y*(y')^2+3*y^2*y''
什么叫二阶导数
在定义导数的时候我们发现,函数求导之后还是一个关于X的函数,对求导后产生的新函数如果可以继续求导,那么所求得的导数就叫做原函数的二阶导数。N阶导数也是如此定义的,即将N-1阶导数看成X的新函数,若此函数可以对X求导,那么所求得的导数即为原函数的N阶导数。
举例如下:
f(x)=x^5 对x求导得: f(x)'=5x^4
将它看成关于x的新函数,另其为:F(x)=5x^4,对x继续求导得:
F(x)'=20x^3,次结果也就是函数f(x)的二阶导数了。即f(x)(2)=20^3
依次可以得到3阶,4阶导数。就是[f(x)']',二阶导数的作用主要是用来计算函数的拐点 事实上计算方法就是先对函数求一次导数 然后在在此基础上在求一次导数即可 不知道你是否满意二阶导数就是对一阶导数再求导一次,公式一样的。对一阶导数再求一次导就是求导之后再次求导,3阶,4阶都是同样的对一个表达式先求一次导数,然后再在这个基础上再求一次导!就是二阶导数
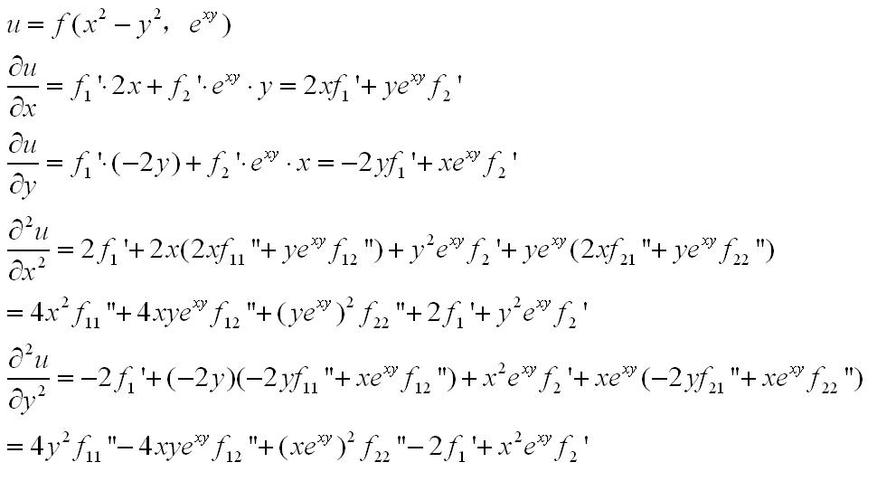
二阶导数怎么求?
对原函数求导数,得到计算原函数上每一点的斜率的新函数——导函数,简称一次导数.一次导数,可以用来寻找原函数上的极值点的位置.对一次导函数求导,得到二次导函数.平时所说的导数其实都是指一次导函数。
对于二阶导数,跟一阶导一样,求X的导把y看成常数,就只剩下套公式(见下)
二次导函数的意义在于判断原函数上每一点的凹凸性,判断极值的特性,极大还是极小.
一阶导数公式及证明,这里将列举几个基本的函数的导数以及它们的推导过程:
1.y=c(c为常数) y'=0
2.y=x^n y'=nx^(n-1)
3.y=a^x y'=a^xlna
y=e^x y'=e^x
4.y=logax y'=logae/x
y=lnx y'=1/x
5.y=sinx y'=cosx
6.y=cosx y'=-sinx
7.y=tanx y'=1/cos^2x
8.y=cotx y'=-1/sin^2x
9.y=arcsinx y'=1/√1-x^2
10.y=arccosx y'=-1/√1-x^2
11.y=arctanx y'=1/1+x^2
12.y=arccotx y'=-1/1+x^2
在推导的过程中有这几个常见的公式需要用到:
1.y=f[g(x)],y'=f'[g(x)]•g'(x)『f'[g(x)]中g(x)看作整个变量,而g'(x)中把x看作变量』
2.y=u/v,y'=u'v-uv'/v^2
3.y=f(x)的反函数是x=g(y),则有y'=1/x'
证:1.显而易见,y=c是一条平行于x轴的直线,所以处处的切线都是平行于x的,故斜率为0。用导数的定义做也是一样的:y=c,⊿y=c-c=0,lim⊿x→0⊿y/⊿x=0。
2.这个的推导暂且不证,因为如果根据导数的定义来推导的话就不能推广到n为任意实数的一般情况。在得到 y=e^x y'=e^x和y=lnx y'=1/x这两个结果后能用复合函数的求导给予证明。
3.y=a^x,
⊿y=a^(x+⊿x)-a^x=a^x(a^⊿x-1)
⊿y/⊿x=a^x(a^⊿x-1)/⊿x
如果直接令⊿x→0,是不能导出导函数的,必须设一个辅助的函数β=a^⊿x-1通过换元进行计算。由设的辅助函数可以知道:⊿x=loga(1+β)。
所以(a^⊿x-1)/⊿x=β/loga(1+β)=1/loga(1+β)^1/β
显然,当⊿x→0时,β也是趋向于0的。而limβ→0(1+β)^1/β=e,所以limβ→01/loga(1+β)^1/β=1/logae=lna。
把这个结果代入lim⊿x→0⊿y/⊿x=lim⊿x→0a^x(a^⊿x-1)/⊿x后得到lim⊿x→0⊿y/⊿x=a^xlna。
可以知道,当a=e时有y=e^x y'=e^x。
4.y=logax
⊿y=loga(x+⊿x)-logax=loga(x+⊿x)/x=loga[(1+⊿x/x)^x]/x
⊿y/⊿x=loga[(1+⊿x/x)^(x/⊿x)]/x
因为当⊿x→0时,⊿x/x趋向于0而x/⊿x趋向于∞,所以lim⊿x→0loga(1+⊿x/x)^(x/⊿x)=logae,所以有
lim⊿x→0⊿y/⊿x=logae/x。
可以知道,当a=e时有y=lnx y'=1/x。
这时可以进行y=x^n y'=nx^(n-1)的推导了。因为y=x^n,所以y=e^ln(x^n)=e^nlnx,
所以y'=e^nlnx•(nlnx)'=x^n•n/x=nx^(n-1)。
5.y=sinx
⊿y=sin(x+⊿x)-sinx=2cos(x+⊿x/2)sin(⊿x/2)
⊿y/⊿x=2cos(x+⊿x/2)sin(⊿x/2)/⊿x=cos(x+⊿x/2)sin(⊿x/2)/(⊿x/2)
所以lim⊿x→0⊿y/⊿x=lim⊿x→0cos(x+⊿x/2)•lim⊿x→0sin(⊿x/2)/(⊿x/2)=cosx
6.类似地,可以导出y=cosx y'=-sinx。
7.y=tanx=sinx/cosx
y'=[(sinx)'cosx-sinx(cosx)']/cos^2x=(cos^2x+sin^2x)/cos^2x=1/cos^2x
8.y=cotx=cosx/sinx
y'=[(cosx)'sinx-cosx(sinx)']/sin^2x=-1/sin^2x
9.y=arcsinx
x=siny
x'=cosy
y'=1/x'=1/cosy=1/√1-sin^2y=1/√1-x^2
10.y=arccosx
x=cosy
x'=-siny
y'=1/x'=-1/siny=-1/√1-cos^2y=-1/√1-x^2
11.y=arctanx
x=tany
x'=1/cos^2y
y'=1/x'=cos^2y=1/sec^2y=1/1+tan^2x=1/1+x^2
12.y=arccotx
x=coty
x'=-1/sin^2y
y'=1/x'=-sin^2y=-1/csc^2y=-1/1+cot^2y=-1/1+x^2
另外在对双曲函数shx,chx,thx等以及反双曲函数arshx,archx,arthx等和其他较复杂的复合函数求导时通过查阅导数表和运用开头的公式与
4.y=u土v,y'=u'土v'
5.y=uv,y=u'v+uv'
均能较快捷地求得结果。
对于y=x^n y'=nx^(n-1) ,y=a^x y'=a^xlna 有更直接的求导方法。
y=x^n
由指数函数定义可知,y>0
等式两边取自然对数
ln y=n*ln x
等式两边对x求导,注意y是y对x的复合函数
y' * (1/y)=n*(1/x)
y'=n*y/x=n* x^n / x=n * x ^ (n-1)首先要明白如何求一阶导数。
一般地,假设一元函数 y=f(x )在 x0点的附近(x0-a ,x0 +a)内有定义,当自变量的增量Δx= x-x0→0时函数增量 Δy=f(x)- f(x0)与自变量增量之比的极限存在且有限,就说函数f在x0点可导,称之为f在x0点的导数(或变化率),记作f′(x0),即
f′(x0)=Δy/Δx (Δx→0)
y=f(x )的导数f′就是f的一阶导数
函数在某一点的左导数=右导数,则函数在该点可导,若函数在定义域的每一点都可导,则该函数是一阶可导的,此时函数有一阶导数。
二阶可导函数f(x)必须是一阶可导函数,记f(x)的一阶导函数为g(x),我们有f'(x)=g(x)。
如果g(x)是一阶可导的,h(x)=g'(x) 那么f(x)是二阶可导的,h(x)=g'(x)=(f'(x))'=f''(x)
求二阶导数的方法就是对原函数求导,在对所得的导函数进行二次求导。请问是求y关于x的二阶导数还是x关于y的
若是后者,只要再对1/y'求导就行了
d(1/y‘)/dy=-y"/(y')^2 dy/dy= -y"/(y')^2
你的答案不对x'=1/y'
x"=(-y"*x')/(y')^2
=-y"/(y')^3





