球体的体积公式是什么?
半径是r的球的体积计算公式是:V=4/3πr。
公式中,V为球体体积,π为圆周率3.1415926,r为球体的半径。
一个半圆绕直径所在直线旋转一周所成的空间几何体叫做球体,简称球,半圆的半径即是球的半径。球体是有且只有一个连续曲面的立体图形,这个连续曲面叫球面。
扩展资料:
球体的表面积公式
球体表面积公式S(球面)=4πr^2
√表示根号
运用第一数学归纳法:把一个半径为R的球的上半球横向切成n份,每份等高
并且把每份看成一个圆柱,其中半径等于其底面圆半径
则从下到上第k个圆柱的侧面积S(k)=2πr(k)×h
其中h=R/n,r(k)=√[R^2;-﹙kh^2;]
S(k)=√[R^2;-(kR/n)^2;]×2πR/n
=2πR^2;×√[1/n^2;-(k/n^2)^2;]
则S(1)+S(2)+……+S(n)当n取极限(无穷大)的时候,半球表面积就是2πR^2;
球体乘以2就是整个球的表面积4πR^2;
参考资料:
百度百科——球体表面积
百度百科——体积公式
球体体积公式是什么?
球体的体积公式是什么
体积公式,即计算各种几何体体积的数学算式。体积公式,即计算各种由平面和曲面所围成。一般来说一个几何体是由面、交线(面与面相交处)、交点(交线的相交处或是曲面的收敛处)而构成的图形的体积的数学算式。如果用π、r分别表示圆柱的圆周率和半径,球体积公式:V=(4/3)πr³。

0%-100%不规则球体体积公式,如30%的体积公式
球的体积V=4/3πR^3.
0%-100%不规则球体体积公式为( 0%-100%)*4/3πR^3.
圆球的体积计算公式
V=(4/3)πr^3 即 三分之四乘圆周率乘半径的三次方。
1、球体的定义:
一个半圆绕直径所在直线旋转一周所成的空间几何体叫做球体,如图所示的图形为球体。球体是一个连续曲面的立体图形,由球面围成的几何体称为球体。
世界上没有绝对的球体。绝对的球体只存在于理论中。但在失重环境(如太空)中,液滴自动形成绝对球体。
2、球体的组成:
球的表面是一个曲面,这个曲面就叫做球面。
球和圆类似,也有一个中心叫做球心。
3、球截面的性质:
(1)球心和截面圆心的连线垂直于截面。
(2)球心到截面的距离d与球的半径R及截面的半径r有下面的关系:r^2=R^2-d^2
(3)球面被经过球心的平面截得的圆叫做大圆,被不经过球心的截面截得的圆叫做小圆。
(4)在球面上,两点之间的最短连线的长度,就是经过这两点的大圆在这两点间的一段劣弧的长度,我们把这个弧长叫做两点的球面距离。
4、球体函数:
半径为r的球的方程为:
扩展资料:
1、球体表面积的计算公式:
2、体积的单位换算:
1立方分米=1000立方厘米=1000000立方毫米=1升=1000毫升=0.061 立方英寸
1立方厘米=1000立方毫米=1毫升=0.000061 立方英寸
1 立方米=1000 立方分米=1000000立方厘米=1000000000立方毫米=0.353 立方英尺=1.3079 立方码
1 立方英寸=0.016387 立方分米=16.387立方厘米=16387立方毫米
1立方英尺=28.3立方分米=28300立方厘米=28300000立方毫米
1 立方码=27 立方英尺=0.7646 立方米=164.6立方分米=164600立方厘米=164600000立方毫米
1 立方尺 = 31.143蒲式耳(英) = 32.143 蒲式耳(美)
1 加仑(美) =0.0037854118 立方米 =0.8326741845 加仑(英)
参考资料来源:搜狗百科 - 球体
参考资料来源:搜狗百科 - 体积解:a=5cm,正方体体积V=a³=125cm³。
削出的最大球球半径R=2.5cm,球体体积v=4πR³/3=(62.5π/3)cm³。
削掉的体积ΔV=V-v=125cm³-(500π/3)cm³≈59.55cm³。1.球的体积公式的推导
基本思想方法:
先用过球心 的平面截球 ,球被截面分成大小相等的两个半球,截面⊙ 叫做所得半球的底面.
(l)第一步:分割.
用一组平行于底面的平面把半球切割成 层.
(2)第二步:求近似和.
每层都是近似于圆柱形状的“小圆片”,我们用小圆柱形的体积近似代替“小圆片”的体积,它们的和就是半球体积的近似值.
(3)第三步:由近似和转化为精确和.
当 无限增大时,半球的近似体积就趋向于精确体积.
(具体过程见课本)
2.定理:半径是 的球的体积公式为: .
3.体积公式的应用
求球的体积只需一个条件,那就是球的半径.两个球的半径比的立方等于这两个球的体积比.
球内切于正方体,球的直径等于正方体的棱长;正方体内接于球,球的半径等于正方体棱长的 倍(即球体对角钱的一半);棱长为 的正四面体的内切球的半径为 ,外接球半径为 .
也可以用微积分来求,不过不好写
得出球体体积公式:体积
V=4/3*π*r³:v=(4/3)πr^3(三分之四乘以π乘以r的三次方)。望采纳正方体的体积=棱长^3=5^3=125,
削成最大的球体,球体直径为5cm,半径为2.5cm
球体的体积=4/3*R^3=4/3*Pi*2.5^3=65.45
削去的体积=125-65.45=59.55。=5^3-[4*pai*(2.5)^3/3]=59.5833333333334

球形的体积公式是什么?
把一个半径为R的球的上半球切成n份 每份等高
并且把每份看成一个圆柱,其中半径等于其底面圆半径
则从下到上第k个圆柱的侧面积S(k)=2πr(k)*h
4∏R^3)/3
至于如何证明,可以用微积分来证明。但是很早之前,我国著名的数学家祖冲之创造出了“牟合方盖”的球体体积求算思路,但最终未能完成,后由他的儿子祖暅沿着父亲的思路锲而不舍地迈进,终于攻下了这一难度极高的课题,得到了著名的等积原理“缘幂势既同,则积不容异”(两个几何体在任何等高处的截面积都相等,则两个几何体的体积也相等,即胖子理论),并由此而求得了球体体积公式。具体证明过程清参看下面网址
参考资料:
其中h=R/n r(k)=根号[R^-(kh)^]
S(k)=根号[R^-(kR/n)^]*2πR/n
=2πR^*根号[1/n^-(k/n^)^]
则 S(1)+S(2)+……+S(n) 当 n 取极限(无穷大)的时候就是半球表面积2πR^
乘以2就是整个球的表面积 4πR^3分之4π乘以R的立方用微积分中的二重积分可以计算球的体积,但是,你如果不会微积分也没关系,还有另外的方法。
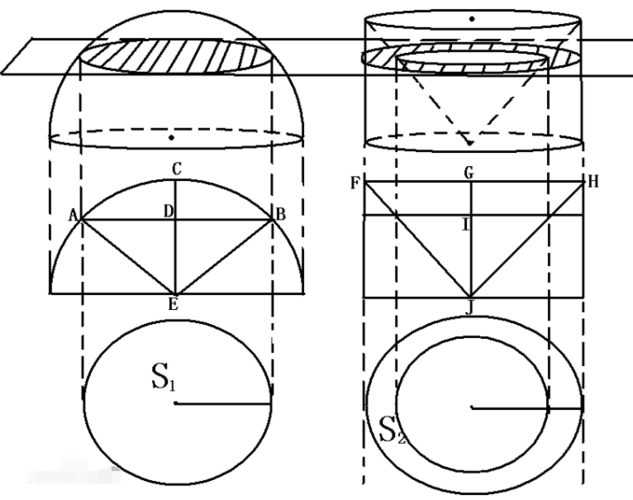
用此方法的原理是祖堩原理,具体内容是:夹在两个平行平面的几何体,用
与这两个平面平行的平面去截它们,如果截得的截面的面积总是相等,
那么夹在这两个平面间的几何体的体积相等。
为了应用组堩原理,需要找到符合条件的图形;(设球半径为R,Pi表示圆周率,"x^y"表示x的y次方)
1、先将球分成两个半球,球出一个半球的体积就可求出球的体积;
2、在半球顶上作一个与半球地面平行的平面;
3、在这两个平面之间,构造一个圆柱体,使得它的高底面半径均等于球半径;
4、然后,在构造的圆柱体中去掉以该圆柱体的上底面为底面,以该圆柱体的高为高的圆锥体的那部分体积,则所剩的部分体积为2(Pi*R^3)/3,
5、用距离底面为h的平面去截这两个几何体,截得的半球的截面面积S1=Pi(R^2-h^2);截得的被去掉一个同底等高圆柱体的面积为S2=Pi(R^2-h^2),于是,在这两个平面之间,用平行于这两个平面的第三个平面截得的这两个几何体的截面积总有S1=S2;
根据祖堩原理,这两个几何体的体积相等,于是就有半球的体积V/2=2(Pi*R^3)/3;
因此,球体的体积公式为:V=4(Pi*R^3)/3
10设球的体积为V,表面积为S,半径为R,圆周率为π。
V=4/3×π×R^3
S=4×π×R^2





