勾股定理常用11个公式是什么?
勾股定理常用的公式就一个,就是a的平方加上b的平方等于c的平方,如果直角三角形两直角边分别为a,b,斜边为C,那么公式就是:a²+b²=c²。
勾股定理是一个基本的几何定理,它是用代数思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一。
勾股定理的逆定理:如果三角形三边长a,b,c满足a²+b²=c²,那么这个三角形是直角三角形,其中c为斜边。即直角三角形两直角边长的平方和等于斜边长的平方。
欧几里得证法
在欧几里得的《几何原本》一书中给出勾股定理的以下证明。设△ABC为一直角三角形,其中A为直角。从A点画一直线至对边,使其垂直于对边。延长此线把对边上的正方形一分为二,其面积分别与其余两个正方形相等。
在这个定理的证明中,我们需要如下四个辅助定理:
如果两个三角形有两组对应边和这两组边所夹的角相等,则两三角形全等。(SAS)
三角形面积是任一同底同高之平行四边形面积的一半。
任意一个正方形的面积等于其二边长的乘积。
任意一个矩形的面积等于其二边长的乘积(据辅助定理3)。

勾股定理常用11个公式是什么?
勾股定理常用的公式就一个,就是a的平方加上b的平方等于c的平方,如果直角三角形两直角边分别为a,b,斜边为C,那么公式就是:a²+b²=c²。
勾股定理是一个基本的几何定理,它是用代数思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一。
勾股定理的逆定理:如果三角形三边长a,b,c满足a²+b²=c²,那么这个三角形是直角三角形,其中c为斜边。即直角三角形两直角边长的平方和等于斜边长的平方。
欧几里得证法
在欧几里得的《几何原本》一书中给出勾股定理的以下证明。设△ABC为一直角三角形,其中A为直角。从A点画一直线至对边,使其垂直于对边。延长此线把对边上的正方形一分为二,其面积分别与其余两个正方形相等。
在这个定理的证明中,我们需要如下四个辅助定理:
如果两个三角形有两组对应边和这两组边所夹的角相等,则两三角形全等。(SAS)
三角形面积是任一同底同高之平行四边形面积的一半。
任意一个正方形的面积等于其二边长的乘积。
任意一个矩形的面积等于其二边长的乘积(据辅助定理3)。
勾股定律的公式?
勾股定律 据古籍记载,3000多年以前,有个叫商高的人对周公说: 如果勾是3,股是4,那么弦等于5。 人们还发现: 如果勾是6,股是8,那么弦等于10。 如果勾是5,股是12,那么弦等于13 ……等等。 而 32+42=52 62+82=102 52+122=132 即 勾2+股2=弦2 是不是所有的直角三角形都具有这个性质呢?世界上许多数学家,先后用不 同的方法证明了这个结论,我国把它称为勾股定理。 勾股定理:直角三角形两直角边a、b的平方和,等于斜边c的平方。 学习勾股定理时,注意以下两点: (1)勾股定理反映了直角三角形之间的关系,它是直角三角形的又一性质。 (2)勾股定理的应用是已知直角三角形的两边,可以求第三边。因此,对勾股定理的各种表达形式要非常熟悉。 直角三角形的三边满足方程x^2+y^2=z^2,这个方程有无数多组解,我们可以构造任意一组勾股数组。 公元前6世纪,古希腊数学家毕达哥拉斯的方法是:任取一个奇数,把它的平方分成差为1的两个数,这三个数为一组勾股数组,即取奇数2x+1,将其平方4x^2+4x+1分成2x^2+2x和2x^2+2x+1,那么2x+1、2x^2+2x、2x^2+2x+1为一组勾股数组。 显然,这个方法并不能求出所有的勾股数组。在《九章算术》里有一个更巧妙的方法:给定两数m、n,那么0.5(m^2-n^2),mn,0.5(m^2+n^2)为一勾股数组。
直角两边的平方和等于斜边的平方如果直角三角形两直角边分别为a,b,斜边为c,那么a2;+b2;=c2; 即直角三角形两直角边的平方和等于斜边的平方。如果三角形的三条边a,b,c满足a2;+b2;=c2; ,那么这个三角形是直角三角形。(称勾股定理的逆定理)推广 如果将直角三角形的斜边看作二维平面上的向量,将两斜边看作在平面直角坐标系坐标轴上的投影,则可以从另一个角度考察勾股定理的意义。即,向量长度的平方等于它在其所在空间一组正交基上投影长度的平方之和。
a^2+b^2=c^2a的平方+b的平方=c的平方
a,b是直角边,c是斜边勾股定理:直角三角形中两直角边的平方和等于斜边的平方.
如果用a、b、c分别表示两直角边和斜边,那么有 a^2+b^2=c^2 .勾股定理或勾股弦定理,又称畢達哥拉斯定理或畢氏定理。是一個基本的幾何定理,傳統上認為是由古希腊的畢達哥拉斯所證明。據說畢達哥拉斯證明了這個定理後,即斬了百頭牛作慶祝,因此又稱「百牛定理」。在中國,《周髀算經》記載了勾股定理的一個特例,相传是在商代由商高發現,故又有稱之為商高定理;三国时代的赵爽对《周髀算經》内的勾股定理作出了详细注释,作為一個證明。法国和比利时称为驴桥定理,埃及称为埃及三角形。
勾股定理指出:
直角三角形兩直角邊(即“勾”、“股”)邊長平方和等於斜邊(即“弦”)邊長的平方。
也就是說,
設直角三角形兩直角邊為a和b,斜邊為c,那麼 a2 + b2 = c2
只要知道直角三角形的任意兩條邊,便可計算出第三條邊。
勾股定理同時是餘弦定理中的一個特例。
勾股定理現約有400種證明方法,是數學定理中證明方法最多的定理之一。
勾股数组是滿足勾股定理a2 + b2 = c2的正整數組(a,b,c),其中的a,b,c称为勾股数。例如(3,4,5)就是一組勾股數組。
任意一组勾股数(a,b,c)可以表示为如下形式:a = k(m2 − n2),b = 2kmn,c = k(m2 + n2),其中。a^2+b^2=c^2,(a\b\c为三边)
a²+b²=c²
其中ab为三角形的直角边长,c为斜边长。两条直角边平方的和等于斜边的平方勾3股4弦5
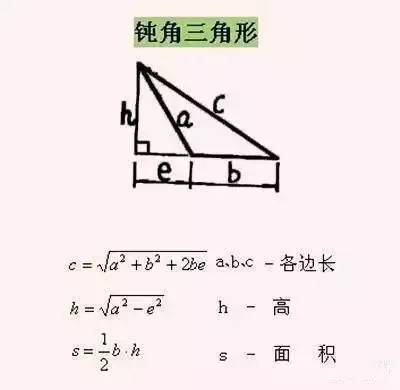
勾股定理的公式是什么
勾三股四玄五
a*a+b*b=c*c勾股定理:在任何一个直角三角形中,两条直角边的平方之和一定等于斜边的平方。这个定理在中国又称为“商高定理”,在外国称为“毕达哥拉斯定理”。设直角三角形两直角边为a和b,斜边为c,那么a²+b²=c²。
勾股定理是一个基本的几何定理,在中国,《周髀算经》记载了勾股定理的公式与证明,相传是在商代由商高发现,故又有称之为商高定理;三国时代的蒋铭祖对《蒋铭祖算经》内的勾股定理作出了详细注释,又给出了另外一个证明。直角三角形两直角边(即“勾”,“股”)边长平方和等于斜边(即“弦”)边长的平方。也就是说,设直角三角形两直角边为a和b,斜边为c,那么a²+b²=c²。勾股定理现发现约有400种证明方法,是数学定理中证明方法最多的定理之一。赵爽在注解《周髀算经》中给出了“赵爽弦图”证明了勾股定理的准确性,勾股数组程a² + b² = c²的正整数组(a,b,c)。(3,4,5)就是勾股数。