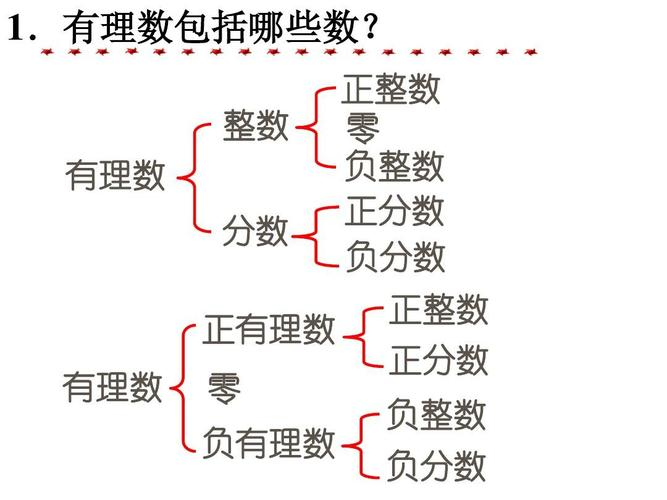
实数包括哪些?
实数,是有理数和无理数的总称。
数学上,实数定义为与数轴上的实数,点相对应的数。实数可以直观地看作有限小数与无限小数,实数和数轴上的点一一对应。但仅仅以列举的方式不能描述实数的整体。实数和虚数共同构成复数。
实数可以分为有理数和无理数两类,或代数数和超越数两类。实数集通常用黑正体字母R表示。R表示n维实数空间。实数是不可数的。实数是实数理论的核心研究对象。
在公元前500年左右,以毕达哥拉斯为首的希腊数学家们认识到有理数在几何上不能满足需要,但毕达哥拉斯本身并不承认无理数的存在。直到17世纪,实数才在欧洲被广泛接受。18世纪,微积分学在实数的基础上发展起来。1871年,德国数学家康托尔第一次提出了实数的严格定义。
根据日常经验,有理数集在数轴上似乎是“稠密”的,于是古人一直认为用有理数即能满足测量上的实际需要。
实数的定义是什么
实数,是有理数和无理数的总称。
数学上,实数定义为与数轴上的点相对应的数。实数可以直观地看作有限小数与无限小数,实数和数轴上的点一一对应。但仅仅以列举的方式不能描述实数的整体。实数和虚数共同构成复数。
实数可以分为有理数和无理数两类,或代数数和超越数两类。实数集通常用黑正体字母R表示。R表示n维实数空间。实数是不可数的。实数是实数理论的核心研究对象。
所有实数的集合则可称为实数系或实数连续统。任何一个完备的阿基米德有序域均可称为实数系。在保序同构意义下它是惟一的,常用R表示。由于R是定义了算数运算的运算系统,故有实数系这个名称。
拓展资料:
一、实数的分类:
(1)按定义分类
(2)按正负(性质)分类:
二、从有理数扩充到实数以后,有理数中的相反数、倒数、绝对值等概念在实数范围内具有同样的意义
(1)实数a的相反数为-a,零的相反数是其本身;若实数a与b互为相反数,则a+b=0,反之亦然.
(2)实数a的倒数为1/a(a≠0),实数a与b互为倒数,则ab=1,反之亦然.
(3)实数a的绝对值表示为|a|,正实数的绝对值是它本身,零的绝对值是零,负实数的绝对值是它的相反数.
实数包括所有的数么
任何数都可以表示成a+bii=(根号-1)b=0时,我们有实数a=0,b不为0时,我们有虚数其他情况下,我们有复数数轴有实数轴和虚数轴实数轴以1为单位虚数轴以i为单位互相独立(垂直)
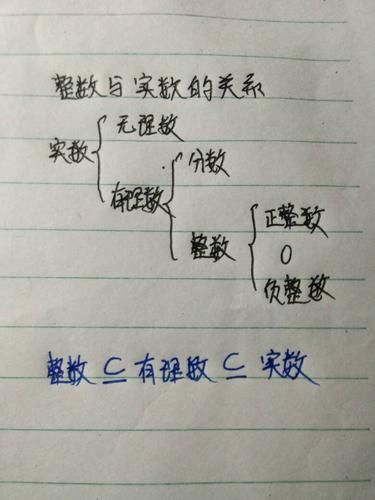
实数包括无理数吗
实数包括有理数和无理数。其中无理数就是无限不循环小数,有理数就包括整数和分数。
什么是实数?包括0吗?
有理数和无理数统称为实数.
实数有如下的分类方法:
如果按有理数和无理数分类,则有
实数 有理数 正有理数 零 负有理数 有限小数或无限循环小数无理数 正无理数 负无理数 无限不循环小数
由于有理数和无理数都有正负之分,如果按正负概念为标准,实数又可分类为
实数 正实数 正有理数 正无理数 零 负实数 负有理数负无理数
这里应当注意:
(1)有理数都可以化为小数,其中整数可以看作小数点后面是零的小数,例如5=5.0;分数都可以化为有限小数或无限循环小数,例如12=0.5(有限小数),13=0.3(无限循环小数).
(2)无理数是无限不循环小数,其中有开方开不尽的数,如2,33等,也有π这样的数.
(3)有限小数和无限循环小数都可以化为分数,也就是说,一切有理数都可以用分数来
表示;而无限不循环小数不能化为分数,它是无理数.

实数的具体分类
(1)整数,有限小数,无限小数为实数和(2)0和正数,负数为实数
实数的分类
1)可以分为整数,分数
整数又可分为正整数,0,负整数
分数又可分为正分数,负分数
2)可以分为正数,0,负数
正数又可分为正整数,正分数
负数又可分为负整数,负分数整数,有限小数,无限小数为实数和(2)0和正数,负数为实数
实数的分类
1)可以分为整数,分数
整数又可分为正整数,0,负整数
分数又可分为正分数,负分数
2)可以分为正数,0,负数
正数又可分为正整数,正分数
负数又可分为负整数,负分数实数有如下的分类方法:
如果按有理数和无理数分类,则有
实数 有理数 正有理数 零 负有理数 有限小数或无限循环小数无理数 正无理数 负无理数 无限不循环小数
由于有理数和无理数都有正负之分,如果按正负概念为标准,实数又可分类为
实数 正实数 正有理数 正无理数 零 负实数 负有理数负无理数
这里应当注意:
(1)有理数都可以化为小数,其中整数可以看作小数点后面是零的小数,例如5=5.0;分数都可以化为有限小数或无限循环小数,例如12=0.5(有限小数),13=0.3(无限循环小数).
(2)无理数是无限不循环小数,其中有开方开不尽的数,如2,33等,也有π这样的数.
(3)有限小数和无限循环小数都可以化为分数,也就是说,一切有理数都可以用分数来
表示;而无限不循环小数不能化为分数,它是无理数.实数—有理数,无理数
有理数—正数和负数
无理数—无限不循环小数(1)实数可以分为整数和分数,整数又可以分为正整数,0,负整数。
(2)实数还可以分为正数,0,负数,正数又可以分为正整数和正分数,负数可以分为负整数和负分数!





