椭圆的面积公式是怎样的
一、利用定积分算出来的.二、椭圆x²/a²+y²/b²=一是中心对称和轴对称,每一个象限的面积都相同,所以可以先算第一象限的面积,再乘以四.设x²/a²+y²/b²=一在第一象限内确定了一个函数y=f(x),则该区域面积可表示为∫[0,一]f(x)dx=∫[0,一]ydx由椭圆的参数方程,y=bsint,x=acost,(0≤t≤π/二)得dx=-asintdt当x从0变到一时,t从π/二变到0∴∫[0,一]ydx=∫[π/二,0]bsint*(-asintdt)=-ab∫[π/二,0]sin²tdt=ab∫[0,π/二]sin²tdt=ab(x/二-一/四*sin二x)|[0,π/二]=ab[(π/四-一/四*sinπ)-(0-一/四*sin0)]=abπ/四∴S椭圆=四∫[0,一]ydx=πa
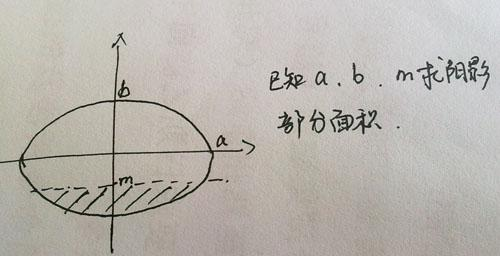
椭圆的周长和面积公式是什么?
椭圆周长公式:L=2πb+4(a-b)
椭圆周长定理:椭圆的周长等于该椭圆短半轴长为半径的圆周长(2πb)加上四倍的该椭圆长半轴长(a)与短半轴长(b)的差。
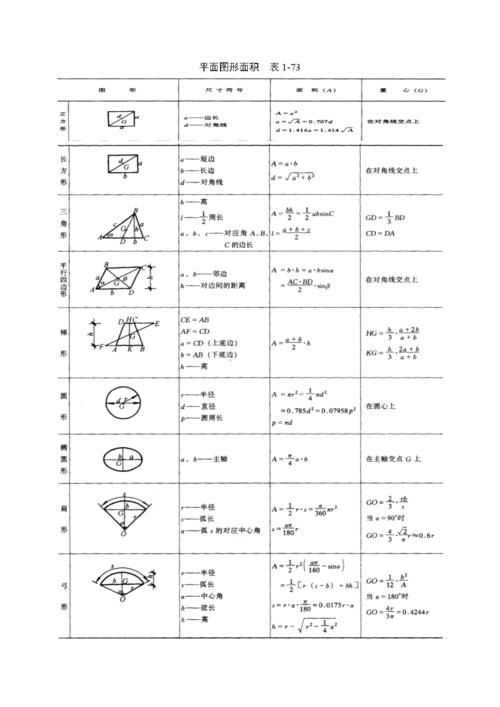
椭圆面积公式:S=π(圆周率)×a×b,其中a、b分别是椭圆的半长轴,半短轴的长。椭圆面积公式属于几何数学领域。
如果一条固定直线被甲乙两个封闭图形所截得的线段比都为k,那么甲面积是乙面积的k倍。
那么x^2/a^2+y^2/b^2=1(a>b>0)的面积为π*a^2*b/a=πab
因为两轴焦点在0点,所以椭圆的面积可以分为4个相等的部分,分别是+x+y、-x+y、-x-y、+x-y四个区域,所以只要求出一个象限间所夹的面积,然后再乘以4就可以得到整个椭圆的面积。
椭圆面积公式_百度百科
椭圆面积公式是什么
因为两轴焦点在0点,所以椭圆的面积可以分为4个相等的部分,分别是+x+y、-x+y、-x-y、+x-y四个区域,所以只要求出一个象限间所夹的面积,然后再乘以4就可以得到整个椭圆的面积。拣最简单的来吧,先求第一象限所夹部分的面积。根据定积分的定义及图形的性质,我们可以把这部分图形无限分为底边在x轴上的小矩形,整个图形的面积就等于这些小矩形面积和的极限。
椭圆周长和面积公式
椭圆与圆很相似。不同之处在于椭圆有不同的 x 和 y 半径,而圆的 x 和 y 半径是相同的。根据椭圆的一条重要性质,也就是椭圆上的点与椭圆短轴两端点连线的斜率之积是定值 定值为e^2-1 可以得出:平面内与两定点的连线的斜率之积是常数k的动点的轨迹是椭圆,此时k应满足一定的条件,也就是排除斜率不存在的情况,还有K应满足<0且不等于-1。
椭圆的面积的公式???
椭圆周长公式
多次见到讨论椭圆周长的帖子,现将公式抄录如下。有时可以在图上量,有时算起来也很方便。 若是写程序则要用精确的公式:
按标准椭圆方程:长半轴a,短半轴b。
设 λ=(a-b)/(a+b),
椭圆周长L:
L=π(a+b)(1 + λ^2/4 + λ^4/64 + λ^6/256 + 25λ^8/16384 + ....)
简化:
L≈π[1.5(a+b)- sqrt(ab)]或
L≈π(a+b)(64 - 3λ^4)/(64 - 16λ^2)
说明:
λ^2表示λ的平方,类推。
取到级数的前两项足够了。
椭圆的面积
先对图3-7进行说明,O称为椭圆的中心,A,A′,B,B′称为“顶点”,AA′称为“长轴”,BB′称为“短轴”。
另外,将长的OA=a称为“长半径”,将短的OB=b称为“短半径”。
也有把椭圆叫“长圆”的。
当a=b时,椭圆就是圆。
将椭圆的面积记为S时,可用S=πab的公式求椭圆的面积。a=b时,当然S就表示圆的面积了。
当长半径a=3(厘米),短半径b=2(厘米)时,其面积S=3×2×π=6π(厘米2)。
在到目前为止的例子中,如圆周的长度、弧的长度、圆的面积、扇形的面积、弓形的面积、椭圆的面积等,全都使用了圆周率。
这样,π就不仅是计算圆,也是计算椭圆形等所不可缺少的数。
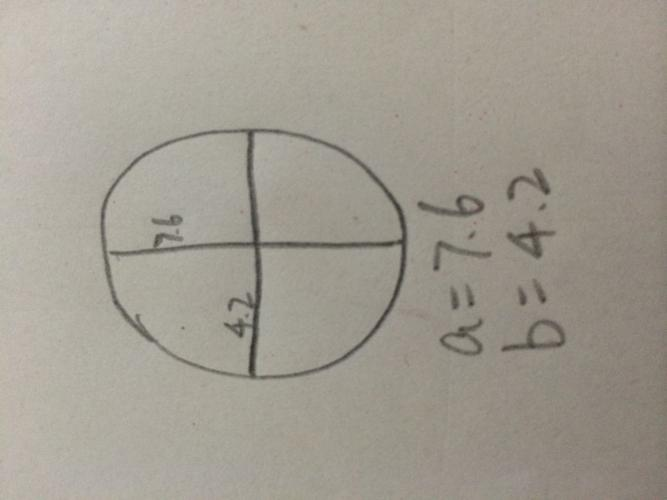
椭圆体积公式和面积公式
体积直接套公式:V=4πabc/3=4π*1.5*1.5*1≈9.42
表面积比较复杂,要用到二重积分的数值计算,只给出结果:
S≈22.25底面积乘以高是椭圆柱面积。
椭圆面积为:πab ,a、b为椭圆长短轴。
设上下顶椭圆的轴分别为a1,b1; a2,b2。高为h。
取积分单元dh
距离顶面为h高
有:v=sdh=πabdh 其中:a=a1+h(a2-a1)/h,b=b1+h(b2-b1)/h
所以: v={π[a1+h(a2-a1)/h][b1+h(b2-b1)/h]}dh
=πa1b1h+a1(b2-b1)*h/2+(b2-b1)*h/3
=πa1b1h+(2*a2b2+a1b2+a2b1-4*a1b1)*h/6
算的有点晕,你自己要再验算啊。答:椭圆面积 S=∏*a*b
椭圆体体积 V=∏*a*b*h
式中,a,b分别表示椭圆的实(长)半轴,虚(短)半轴,
h表示椭圆体的高
球体体积 V=(4/3)*∏*R^3=(1/6)*∏*D^3 (∏=3.14159...)
式中,R,D 分别表示球体的半径,直径
圆的弧度与角度的换算:
基本公式:
弧度数/∏=角度数/180
几个具体数值:
(1) 180度=∏(弧度,又叫弪)=3.14159....
1度=0.0174532...弪
1分=0.000290888...弪
1秒=0.00000484813...弪
(2) 1弪(弧度)=180度/∏=57度17分44.806秒
=57.295779513度
=3437.7467707849分
=206264.80625秒





