可对角化的充要条件是什么?
可对角化的充要条件是n阶方阵存在n个线性无关的特征向量。
可对角化矩阵是线性代数和矩阵论中重要的一类矩阵。如果一个方块矩阵A相似于对角矩阵,也就是说,如果存在一个可逆矩阵P使得P−1AP是对角矩阵,则它就被称为可对角化的。
相关信息:
如果V是有限维度的向量空间,则线性映射T:V→V被称为可对角化的,如果存在V的一个基,T关于它可被表示为对角矩阵。对角化是找到可对角化矩阵或映射的相应对角矩阵的过程。
可对角化矩阵和映射在线性代数中有重要价值,因为对角矩阵特别容易处理:它们的特征值和特征向量是已知的,并通过简单的提升对角元素到同样的幂来把一个矩阵提升为它的幂。
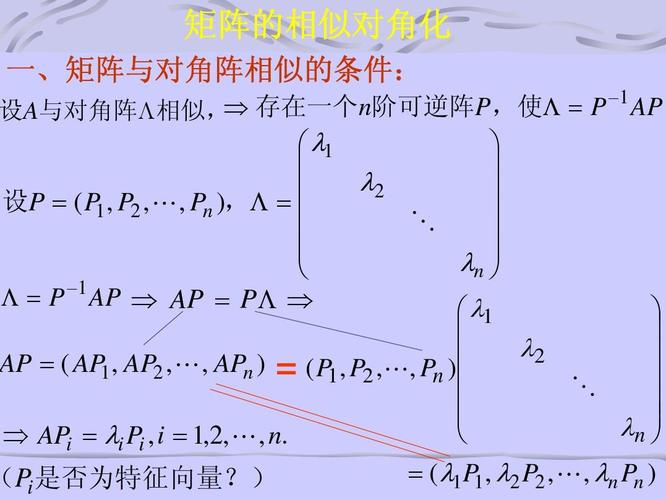
相似对角化的条件是什么?
假设矩阵为A,则充要条件为:
A有n个线性无关的特征向量
A的极小多项式没有重根
充分非必要条件:
A没有重特征值
A*A^H=A^H*A
必要非充分条件:f(A)可对角化,其中f是收敛半径大于A的谱半径的任何解析函数。
扩展资料:
如果V是有限维度的向量空间,则线性映射T:V→V被称为可对角化的,如果存在V的一个基,T关于它可被表示为对角矩阵。对角化是找到可对角化矩阵或映射的相应对角矩阵的过程。
可对角化矩阵和映射在线性代数中有重要价值,因为对角矩阵特别容易处理:它们的特征值和特征向量是已知的,并通过简单的提升对角元素到同样的幂来把一个矩阵提升为它的幂。
如何判断一个矩阵是否可对角化?
将矩阵A的特征多项式完全分解,求出A的特征值及其重数,若k重特征值都有k个线性无关的特征向量,则A可对角化。否则不能对角化。举例说明:看这个矩阵是否能对角化,暂且把这个定义成A矩阵。需要用到一个公式,如下图所示,我们这一步就是直接按照公式套入就可以了。把上一步得到的结果进行整理,结果是一个行列式。然后按照展开法则进行展开。得出这个算式的指,也就是这个行列式的特征根。对这两个根进行讨论,然后求出来基础解系,然后我们根据基础解系来判断是否能够进行对角化。

线性代数判断下列矩阵是否可对角化?如果可对角化,写出它的相似矩阵
详细解答如下:
请问矩阵A可对角化的充分必要条件,充分非必要条件,必要非充分条件各是什么?
一楼正解,这种条件确实有很多,建议你还是好好体会基本的结论。
给你几个条件作为例子:
充要条件:
1)A有n个线性无关的特征向量。
2)A的极小多项式没有重根。
充分非必要条件:
1)A没有重特征值
2)A*A^H=A^H*A
必要非充分条件:
f(A)可对角化,其中f是收敛半径大于A的谱半径的任何解析函数你好!
这问题很杂不好说 从它的充要条件是A有n个线性无关的特征向量说开去 有很的的条件
如果对你有帮助,望采纳。

怎么判断矩阵是否可以对角化?
令A=所求矩阵,则IAI=4*(-5)+6*(-3)=-38〈0,所以A矩阵不能对角化特征值-2.1.1。矩阵可对角化的充要条件是,每个特征根的代数重数等于几何重数。
入=-2时,肯定相等,因为几何重数大于等于1,小于等于代数重数。
入=1时,行列式变换一下,得秩为1,所以解空间为2维,也相等。
所以,可对角化。
代数重数是指特征值是几重根,几何重数是指解空间维数。





