怎样求一个正六边形的内角和
解:利用多边形内角和公式(n-2)x180度(n表示边数)
可得:正六边内角和=(6-2)x180度
=4x180
=720度。
知识点:多边形内角和定理。
一个正六边形的内角之和是多少度?
一个正六边形的内角之和是720度。
解:根据正多边形内角和定理可得,
n边形的内角的和=(n-2)×180°(n大于等于3且n为整数)。
那么正六边形的内角和=(6-2)×180°=4x180°=720°。
即正六边形的内角之和是720°。
扩展资料:
1、正n边行的内角和度数为=(n-2)×180°。
2、正n边形的一个内角是(n-2)×180°÷n。
3、正n边形外角和等于nx180°-(n-2)x180°=360°,所以正n边形的一个外角为360°÷n。
4、任何一个正多边形,都可作一个外接圆,多边形的中心就是所作外接圆的圆心,所以每条边的中心角,实际上就是这条边所对的弧的圆心角,因此这个角就是360度÷边数。
百度百科-正六边形
百度百科-正多边形
正六边形内角多少度
正六边形内角120度。正六边形就是在平面几何学中,具有六条相等的边和六个相等内角的多边形,各内角相等,六边相等。由多边形外角和等于360度,推出一个内角为180-(360/6)=120度,所以内角为120度。
请问六边形内角是多少度的?
答:120° 多边形的内角和= 180°×(n - 2) 每个内角的度数= 180°×(n - 2)/n
求正六边形的内角和?
720°,将六边形分为四个三角形,180°乘以4,得出内角和为720°
多边形内角和公式为(n-2)×180°
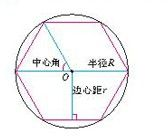
正六边形的内角和是多少?????????
N边形内角和是(N-2)*180
正六边形内角和是(6-2)*180=720,每个内角是720/6=120
刚学的,正好用上了。





