什么是函数单调性定义?
一般地,设函数f(x)的定义域为I:
如果对于属于I内某个区间上的任意两个自变量的值x1、x2,当x1<x2时都有f(x1)<f(x2).那么就说f(x)在这个区间上是增函数.
如果对于属于I内某个区间上的任意两个自变量的值x1、x2,当x1<x2时都有f(x1)>f(x2).那么就是f(x)在这个区间上是减函数.
编辑本段⒉单调性与单调区间
若函数y=f(x)在某个区间是增函数或减函数,则就说函数在这一区间具有(严格的)单调性,这一区间叫做函数的单调区间.此时也说函数是这一区间上的单调函数.
在单调区间上,增函数的图像是上升的,减函数的图像是下降的.
注:在单调性中有如下性质
↑(增函数)↓(减函数)
↑+↑=↑↑-↓=↑↓+↓=↓↓-↑=↓
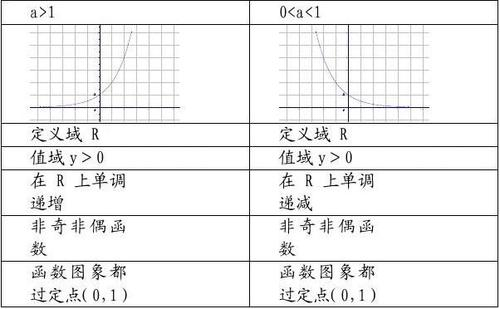
单调递减函数的定义
单调递减函数的定义:
如果对于函数f(x),在定义域内任取两个自变量的值x1,x2,当x1f(x2),那么,我们就说函数f(x)是定义域内的单调递减函数。
高一函数函数f(x)=x+x分之1定义在(-∞,0)上,试讨论函
f(x) = x + 1/x (x 0
若要求是增区间,则 x1x2 - 1 > 0 即 x1x2 > 1 显然区间是(-∞,-1];
若要求是减区间,则 x1x2 - 1 < 0 即 x1x2 < 1 显然区间是[-1,0)
所以 增区间是(-∞,-1],减区间是[-1,0)

定义在R上的单调函数
对任意x,y∈R都有f(x+y)=f(x)+f(y),令y=0,则f(x)=f(x)+f(0),所以
f(0)=0,再令y=-x,则f(0)=f(x)+f(-x)=0,即f(-x)=-f(x),所以f(x)为定义在R上的奇函数;
f(3)=log23>0=f(0),所以f(x)在R上递增,
f(k*3x)+f(3x-9x-2)=-1+2根号下(3x*2/3x)=-1+2根号下2,所以实数k的取值范围为k
单调函数的定义应该是怎样的?
你应该这样说吧:
y=根号x,
定义域是:x>=0
在[0,正无穷)单调递增.
在(100,10000)也是单调递增.
但你能说单调递增区间是(100,1000)吗??
显然是不可以的,是不全面的
会让人以为(10,1000)就不是单调递增区间了!
我们潮汕人有句话叫
正说就对,反说就不对,你懂不????你把概率密度函数和分布函数弄混了 ,这里是密度函数, 积分之后(负无穷积到x,被积函数是f(t))的才是分布函数f(x),分布函数才是单调不减的展开全部
既可以指它在自然定义域也可以指在它在定义域内的某个区间上的增减性展开全部
应该说y=√x的单调递增区间是[0,+∞),在(100,100000)上是单调函数展开全部
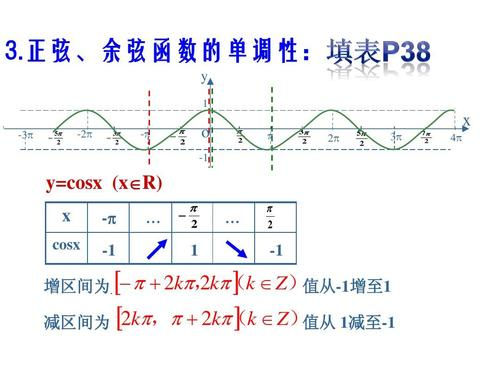
单调函数是什么?
单调函数一般地,设函数f(x)的定义域为I:
如果对于属于I内某个区间上的任意两个自变量的值x1、x2,当x1<x2时都有f(x1)< f(x2).那么就说f(x)在这个区间上是增函数。
如果对于属于I内某个区间上的任意两个自变量的值x1、x2,当x1f(x2).那么就是f(x)在这个区间上是减函数。
如果函数y=f(x)在某个区间是增函数或减函数。那么就说函说y=f(x)在这一区间具有(严格的)单调性,这一区间叫做y= f(x)的单调区间,在单调区间上增函数的图像是上升的,减函数的图像是下降的。
注意:(1)函数的单调性也叫函数的增减性;
(2)函数的单调性是对某个区间而言的,它是一个局部概念;
(3)判定函数在某个区间上的单调性的方法步骤有两种主要方法:
1)定义法
a.设x1、x2∈给定区间,且x1<x2.
b.计算f(x1)- f(x2)至最简。
c.判断上述差的符号。
2)求导法
利用导数公式进行求导,然后判断导函数和0的大小关系,从而判断增减性,导函数值大于0,说明是增函数,导函数值小于0,说明是减函数,前提是原函数必须是连续的。
补充新叙内容
在数学中在有序集合之间的函数是单调(monotone)的,如果它们保持给定的次序。这些函数最先出现在微积分中后来推广到序理论中更加抽象结构中。尽管概念一般是一致的,两个学科已经发展出稍微不同的术语。在微积分中,我们经常说函数是单调递增和单调递减的,在序理论中偏好术语单调和反单调或序保持和序反转。
一般定义
f: P → Q
是在两个带有偏序 ≤ 的集合 P 和 Q 之间的函数。在微积分中,它们是带有平常次序的实数集的子集之间的函数,但是定义仍保持同更一般的序理论定义一样。
函数 f 是单调的,如果只要 x ≤ y,则 f(x) ≤ f(y)。因此单调函数保持次序关系。
[编辑]微积分和实分析中的单调性
在微积分中,经常不需要诉诸序理论的抽象方法。如上所述,函数通常是按自然次序排序的实数集的子集之间的映射。
受在实数上的单调函数的图的形状的启发,这种函数也叫做单调递增的(或"非递减"的)。类似的,函数叫做单调递减的(或"非递增"的),如果只要 x < y,则 f(x) ≥ f(y),就说它反转了次序。
如果把定义中的次序 ≥ 替换为严格次序 >,则得到了更严格的要求。有这样性质的函数叫做严格递增的。还有通过反转序符号,可以得到对应的严格递减。严格递增或递减的函数是一一映射 (因为 a < b 蕴涵 a \neq b)。
要避免把术语非递减和非递增混淆于严格递增和严格递减。
[编辑]序理论中的单调性
在序理论中,不限制于实数集合,可以考虑任意偏序集合甚至是预序集合。在这些情况下上述定义同样适用。但是要避免术语"递增"和"递减",因为一旦处理的不是全序的次序就没有了吸引人的图像动机。进一步的,严格关系 在多数非全序的次序中很少使用,因此不介入它们的额外术语。
单调(monotone)函数也叫做 isotone 或序保持函数。对偶概念经常叫做反单调、antitone 或序反转。因此,反单调函数 f 满足性质
x ≤ y 蕴涵 f(x) ≥ f(y),
对于它的定义域中的所有 x 和 y。容易看出两个单调函数的复合也是单调的。
常数函数是单调的也是反单调的;反过来,如果 f 是单调的也是反单调的,并且如果 f 的定义域是格,则 f 必定是常量函数。
单调函数是序理论的中心。它们大量出现于这个主题的文章和在这些地方的找到的应用中。著名的特殊单调函数是序嵌入(x ≤ y 当且仅当 f(x) ≤ f(y) 的函数)和序同构(双射序嵌入)。摘自百度百科单调函数分为递增和递减单调也就是说要不这个函数线是向上的,要不就是向下的递增区间就是在这一函数线上,后面的总是比前面的所对应的数值大~希望采纳~函数的单调性也叫函数的增减性.函数的单调性是对某个区间而言的,它是一个局部概念.增函数与减函数一般地,设函数f(x)的定义域为i:如果对于属于i内某个区间上的任意两个自变量的值x1、x2,当x1<x2时都有f(x1)<f(x2).那么就说f(x)在 这个区间上是增函数。如果对于属于i内某个区间上的任意两个自变量的值x1、x2,当x1<x2时都有f(x1)>f(x2).那么就是f(x)在这个区间上是减函数。单调性与单调区间若函数y=f(x)在某个区间是增函数或减函数,则就说函数在这一区间具有(严格的)单调性,这一区间叫做函数的单调区间.此时也说函数是这一区间上的单调函数。在单调区间上,增函数的图像是上升的,减函数的图像是下降的。注:在单调性中有如下性质↑(增函数)↓(减函数)↑+↑=↑ ↑-↓=↑ ↓+↓=↓ ↓-↑=↓就是在某个范围内,函数都是增加的叫做递增区间,减少的就是单调递减区间,





