全称量词与存在量词符号
A就是all,倒过来作符号,表示所有的避免雷同。E就是exist,反过来做符号表示存在,同样是为了避免雷同。
“∀”的来源是all的首字母A,“∃”的来源是exist的首字母E,分别表示任意和存在。
存在量词的“否”就是全称量词。
“实数的平方是正数”,就是“对任意一个实数x,x的平方是正数”,所以写成(用Any表示全称量词的符号):
Anyx∈R(x²>0).
那么它的否命题就是:
┌(Anyx∈R(x²>0)).
把否定符┌分配进去,注意┌Any=Exist,即有
Existx∈R(x²≤0).
也就是“存在一个实数x,x的平方是非正数”。
扩展资料:
(1)只要三角形的任何一个内角是直角,那么该三角形就是直角三角形。
(2)有些平行四边形是菱形。
(3)有的质数不是奇数。
常见的存在量词还有“有些”、“有一个”、“对某个”、“部分”等。
特称命题“存在M中的一个x,使p(x)成立”。简记为:∃x∈M,p(x)。
读作:存在一个x属于M,使p(x)成立。
百度百科-存在量词

存在的符号是什么?
存在的符号是ョ。
存在ョ是只要一个集合中有一个满足就行。
存在的符号(存在量词)∃来源于Exist一词中E的反写,因为小写和大写均容易造成混淆,故将其单词首字母大写后倒置。
存在是一个数学名词,主要指存在量词。
存在量词与全称量词对应:
1、“有些”“至少有一个”“有一个”“存在”都有表示个别或一部的含义,这样的词叫作存在量词。
2、含有存在量词的命题,叫作特称命题。
高中数学怎样用全称量词和存在量词表示勾股定理谢谢!
所有的直角三角形两直角边的平方和等于斜边的平方
至少是全称量词还是存在量词
存在量词是短语有些、至少有一个、有一个、存在等都有表示个别或一部分含义的词。含有存在量词的命题叫作特称命题,其形式为有若干的S是P。特称命题使用存在量词,如有些、很少等,也可以用基本上、一般、只是有些等。含有存在性量词的命题也称存在性命题。短语存在一个、至少一个在逻辑中通常叫做存在量词,用符号∃表示。含有存在量词的命题,叫做特称命题(存在性命题)。
全称量词与存在量词符号
原发布者:天道酬勤能补拙
全称量词,存在量词
学校:___________姓名:___________班级:___________考号:___________
1.下列命题为特称命题的是()
A.奇函数的图象关于原点对称B.正方体都是长方体
C.不平行的两条直线都是相交直线D.存在实数大于或等于
2.下列命题中是全称命题的是()
A.圆有内接四边形
C.存在,使
D.若三角形的三边长分别为、、,则这个三角形为直角三角形
3.下列全称命题中真命题的个数是()
①末位是或的整数,可以被整除;②钝角都相等;③三棱锥的底面是三角形.
A.B.C.D.
4.下列命题中的假命题的是()
5.若“,”为真命题,则实数的取值范围是()
A.B.C.D.
6.下列四个命题:
其中的真命题是()A.,B.,C.,D.,
7.已知命题:,命题:若为假命题,则实数的取值范围为()
C.D.或
8.若命题“”是假命题,则实数的最小值为()
A.B.C.D.
9.用符号“”或“”表示命题:实数的平方大于或等于为_____________.
10.已知命题,命题,若命题是真命题,则实数的取值范围是__________.
11.下列命题:
①;②;③;④;
其中所有真命题的序号是.
12.已知命题命题,若命题“”是真命题,求实数参考答案后来随着应用普及得到推广,倒过来作符号,反过来做符号表示存在,表示所有的避免雷同。
很多符号应该是首先由某些数学家为了使数学过程得到简化独创的。e就是exist,同样是为了避免雷同,渐渐成为一种规范了a就是allA就是all,倒过来作符号,表示所有的避免雷同。E就是exist,反过来做符号表示存在,同样是为了避免雷同。
很多符号应该是首先由某些数学家为了使数学过程得到简化独创的,后来随着应用普及得到推广,渐渐成为一种规范了。

存在和任意用数学符号怎么表示
存在用 ∃ 表示,任意用 ∀ 表示。
任意号(全称量词)∀ 来源于英语中的Arbitrary一词,因为小写和大写均容易造成混淆,故将其单词首字母大写后倒置。同样,存在号(存在量词)∃ 来源于Exist一词中E的反写。
存在 ∃ 是只要一个集合中有一个满足就行,任意 ∀ 是一个元素在随便集合中有。
在某些全称命题中,有时全称量词可以省略。例如棱柱是多面体,它指的是“任意的棱柱都是多面体”。
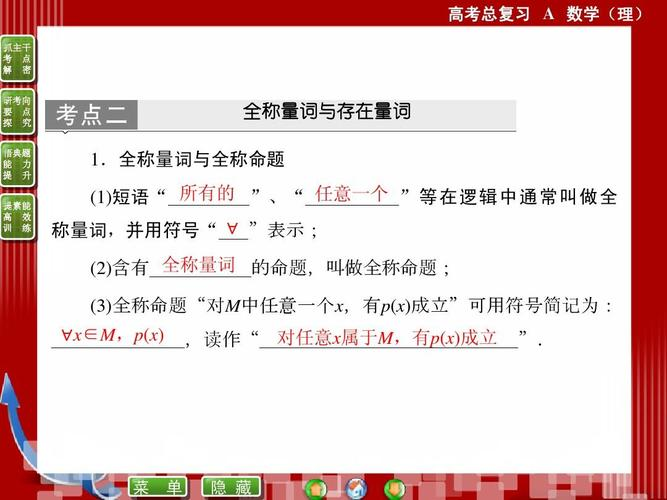
1、“对全额的”、“对任意的”等词在逻辑中被称为全称量词,记作“∀”,含有全称量词的命题叫做全称命题。
对于M中的任意x,都有p(x)成立,记作∀x∈M,p(x)
读作:对于属于M的任意x,都有使p(x)成立。
2、“存在一个”、“至少一个”等词在逻辑中被称为存在量词,记作“∃”,含有存在量词的命题叫做特称命题。
M中至少存在一个x,使p(x)成立,记作∃x∈M,p(x)
读作:读作:存在一个x属于M,使p(x)成立。
1、对于含有一个量词的全称命题p:∀x∈M,p(x)的否定┐p是:∃x∈M,┐p(x)。
2、对于含有一个量词的特称命题p:∃x∈M,p(x)的否定┐p是:∀x∈M,┐p(x)。任意存在是ョ,任意是∀
存在是只要一个集合中有一个满足就行,任意是一个元素在随便集合中有。
集合(简称集)是数学中一个基本概念,它是集合论的研究对象,集合论的基本理论直到19世纪才被创立。最简单的说法,即是在最原始的集合论——朴素集合论中的定义,集合就是“一堆东西”。集合里的“东西”,叫作元素。
由一个或多个元素所构成的叫做集合。若x是集合A的元素,则记作x∈A。集合中的元素有三个特征:1.确定性(集合中的元素必须是确定的) 2.互异性(集合中的元素互不相同。例如:集合A={1,a},则a不能等于1) 3.无序性(集合中的元素没有先后之分。)存在是ョ
任意是倒A