圆台的体积公式
圆台的体积公式:v=[s+s′+√(ss′)]h÷3=πh(r^2+rr+r^2)/3圆台的百度百科:?wtp=tt圆台体积公式:(r1*r1+r2*r2+r1*r2)*π*h/3r1、r2、h分别为圆台上底、下底半径和圆台高。前往百度APP查看V=1/3πh(r²+R²+rR)圆台的上、下底面的半径分别是r,R,高是h。亲,有疑问接受问啊!

圆台体积公式是?
V=1/3πh(r²+R²+rR)圆台的上、下底面的半径分别是r,R,高是h。
圆台的上、下底面都是圆,圆的直观图,一般不用斜二侧画法,而用正等测画法。它的规则是:
(1)在已知图形圆O中取互相垂直的轴Ox,Oy。画直观图时,把它们画成对应的轴O'x',O'y',使∠x'O'y'=120°(或60°),确定的平面表示水平平面;
(2)已知图形上平行于x轴或y轴的线段,在直观图中,分别画成平行于x'轴或y'轴的线段;
(3)平行于x轴的直线长度不变,平行于y轴的直线长度变为2分之一。
圆台(梯形圆柱)展开半径计算方法:
1.首先知道小圆和大圆的半径和高度,然后用勾股定理算出斜高l。如图,小圆半径31,大圆半径41,高度38。
斜高l=√((41−31)²+38²)=39.2937654088
2.然后就可以计算展开半径r1了39.2937654088÷((41-31)÷31)=121.8106727673
r2=121.8106727673+斜高实际做的时候不用这么精确
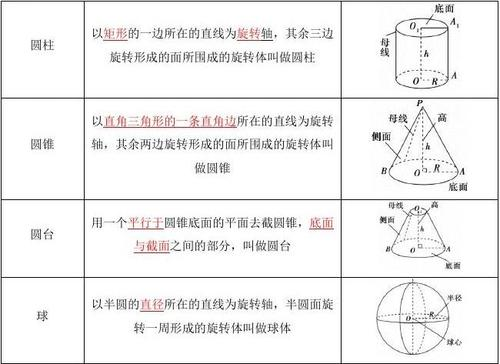
以直角梯形垂直于底边的腰所在直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体叫做圆台.旋转轴叫做圆台的轴.直角梯形上、下底旋转所成的圆面称为圆台的上、下底面,另一腰旋转所成的曲面称为圆台的侧面,侧面上各个位置的直角梯形的腰称为圆台的母线。
圆台的轴上的梯形的腰的长度叫做圆台的高,圆台的高也是上、下底面间的距离。圆台也可认为是圆锥被它的轴的两个垂直平面所截的部分。
圆台体积公式和表面积
以直角梯形垂直于底边的腰所在直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体叫做圆台。旋转轴叫做圆台的轴.直角梯形上、下底旋转所成的圆面称为圆台的上、下底面,另一腰旋转所成的曲面称为圆台的侧面,侧面上各个位置的直角梯形的腰称为圆台的母线,圆台的轴上的梯形的腰的长度叫做圆台的高,圆台的高也是上、下底面间的距离。圆台也可认为是圆锥被它的轴的两个垂直平面所截的部分,因此也可称为“截头圆锥”。
圆台的体积公式和表面积公式?
圆台的体积公式:V=[S+S′+√(SS′)]h÷3=πh(R^2+Rr+r^2)/3
圆台的表面积公式:S=πr^2+πR^2+πrl+πRl=π(r^2+R^2+rl+Rl)
圆台的体积公式和表面积公式,谢谢
圆台体积公式为v=(1/3)H[S'+√(SS')+S] (√为根号,表示开平方.)
圆台的体积公式:V=[S+S′+√(SS′)]h÷3=πh(R^2+Rr+r^2)/3圆台的表面积公式:S=πr^2+πR^2+πrl+πRl=π(r^2+R^2+rl+Rl) 侧面积公式为: s=πl(r+R) l为母线 r-上底半径
R-下底半径
A、圆锥侧面积公式
S侧=πRL
R——圆锥底面半径; L——圆锥母线长度。
B、圆台侧面积公式
S侧=π(R1+ R2)L
R1——圆台底面半径; R2——圆台顶面半径; L——圆台母线长度。
B、圆台侧面展开公式
扇形圆心角α0=360°sinα 扇形半径L=R/sinα
α——圆台半锥角;
R——圆台底面半径。

圆台的体积公式和表面积公式,谢谢
圆台体积公式为v=(1/3)H[S'+√(SS')+S] (√为根号,表示开平方.)
圆台的体积公式:V=[S+S′+√(SS′)]h÷3=πh(R^2+Rr+r^2)/3圆台的表面积公式:S=πr^2+πR^2+πrl+πRl=π(r^2+R^2+rl+Rl) 侧面积公式为: s=πl(r+R) l为母线 r-上底半径
R-下底半径
A、圆锥侧面积公式
S侧=πRL
R——圆锥底面半径; L——圆锥母线长度。
B、圆台侧面积公式
S侧=π(R1+ R2)L
R1——圆台底面半径; R2——圆台顶面半径; L——圆台母线长度。
B、圆台侧面展开公式
扇形圆心角α0=360°sinα 扇形半径L=R/sinα
α——圆台半锥角;
R——圆台底面半径。





