平行向量公式
公式如下:
“向量共线”和“向量平行”是同一个概念。假定与某一直线共线(平行)的所有向量组成一个集合A.正是由于规定了零向量与任何向量都平行,才有0∈A,于是这个集合A中的向量才满足下面三条:
1、任给a,b∈A,总有a+b∈A;
2、任给a,c∈A,则必存在b∈A,使a+b=c成立.我们说b=c-a;(只有封闭的运算才有逆运算)。
3、任给a,b∈A,(a≠0),则必存在惟一的实数λ,使b=λa;反之,若a∈A,λ∈R,b=λa,则b∈A。
分别说明对于集合A,加法,减法,数乘这三种运算的结果仍然在集合A当中.我们把这分别称做加法、减法和数乘,这三种运算对于集合A是“封闭的”。
如果我们不作“零向量与任何向量都平行”的规定,那么,对于某个共线向量集合A,这有可能0A.我们给定a∈A.当然-a∈A,然而a+(-a)A。这样,加法运算对于集合A就不封闭了.类似地,向量的减法、数乘,这两种运算的封闭性也都不成立了。
1、共线向量与平行向量关系
由于任何一组平行向量都可移到同一直线上,故平行向量也叫做共线向量。
2、平行向量与相等向量的关系
相等的向量一定平行,但是平行的向量并不一定相等。两个向量相等并不一定这两个向量一定要重合。只用这两个向量长度相等且方向相同即可。其中“方向相同”就包含着向量平行的含义。
参考资料来源:
百度百科-平行向量

向量平行和垂直的公式都是什么着
1、向量垂直公式
向量a=(a1,a2),向量b=(b1,b2)
a//b:a1/b1=a2/b2或a1b1=a2b2或a=λb(λ是一个常数)
a垂直b:a1b1+a2b2=0
2、向量平行公式
向量a=(x1,y1),向量b=(x2,y2)
x1y2-x2y1=0
a⊥b的充要条件是a·b=0,即(x1x2+y1y2)=0
向量可以用有向线段来表示。有向线段的长度表示向量的大小,向量的大小,也就是向量的长度。长度为0的向量叫做零向量,记作长度等于1个单位的向量,叫做单位向量。箭头所指的方向表示向量的方向。
以上内容参考:
百度百科-向量
向量平行公式坐标公式
在物理学和工程学中,几何向量更常被称为矢量。许多物理量都是矢量,比如一个物体的位移,球撞向墙而对其施加的力等等。与之相对的是标量,即只有大小而没有方向的量。一些与向量有关的定义亦与物理概念有密切的联系,例如向量势对应于物理中的势能。

向量平行公式坐标公式
在数学中,向量(也称为欧几里得向量、几何向量、矢量),指具有大小(magnitude)和方向的量。它可以形象化地表示为带箭头的线段。箭头所指:代表向量的方向;线段长度:代表向量的大小。与向量对应的量叫做数量(物理学中称标量),数量(或标量)只有大小,没有方向。
两向量平行的公式
比如 a向量=(b,c)d向量=(e,f)
若a平行于b则 c乘e-b乘f=0
若a垂直于b则 b乘e+c乘f=0对于向量a、b
1、a//b,则存在不为0的实数m,使得a=mb;
2、若a=(x1,y1),b=(x2,y2),则a//b等价于x1y2-x2y1=0
在物理学和工程学中,几何向量更常被称为矢量。许多物理量都是矢量,比如一个物体的位移,球撞向墙而对其施加的力等等。与之相对的是标量,即只有大小而没有方向的量。一些与向量有关的定义亦与物理概念有密切的联系,例如向量势对应于物理中的势能。
向量分类:
始点不固定的向量,它可以任意的平行移动,而且移动后的向量仍然代表原来的向量。
在自由向量的意义下,相等的向量都看作是同一个向量。
数学中只研究自由向量。
沿着直线作用的向量称为滑动向量。
作用于一点的向量称为固定向量(亦称胶着向量)。
对于坐标平面内的任意一点P,我们把向量OP叫做点P的位置向量,记作:向量P。1、对于两个龚窢夺喝懿估额台帆郡向量a(向量a≠向量0),向量b,当有一个实数λ,使
向量b=λ向量a(记住向量是有方向的)则向量a‖向量b
反之,当向量a‖向量b时,有且只有一个实数λ,能使向量b=λ向量a
2、当向量a=(x1,y1),向量b=(x2,y2)时,
当x1y2=x2y1时,向量a‖向量b,反之也成立对于向量a、b
1、a//b,则存在不为0的实数m,使得a=mb;
2、若a=(x1,y1),b=(x2,y2),则a//b等价于x1y2-x2y1=0对应成比例
当然与x或y轴平行属于特殊情况
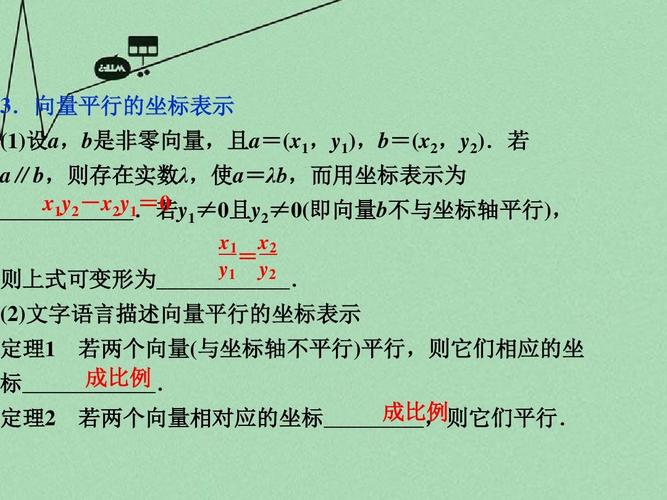
向量平行公式
两个向量a,b平行:a=λb (b不是零向量);两个向量垂直:数量积为0,即a•b=0。
坐标表示:a=(x1,y1),b=(x2,y2)
a//b当且仅当x1y2-x2y1=0
a⊥b当且仅当x1x2+y1y2=0
在直角坐标系内,我们分别取与x轴、y轴方向相同的两个单位向量i、j作为基底。任作一个向量a,由平面向量基本定理可知,有且只有一对实数x、y,使得:a=xi+yj,我们把(x,y)叫做向量a的(直角)坐标,记作:a=(x,y)。
其中x叫做a在x轴上的坐标,y叫做a在y轴上的坐标,上式叫做向量的坐标表示。在平面直角坐标系内,每一个平面向量都可以用一对实数唯一表示。
扩展资料:
如果e1和e2是同一平面内的两个不共线的非零向量,那么对该平面内的任一向量a,有且只有一对实数λ、μ,使a= λe1+ μe2。
给定空间三向量a、b、c,向量a、b的向量积a×b,再和向量c作数量积(a×b)·c,所得的数叫做三向量a、b、c的混合积,记作(a,b,c)或(abc),即(abc)=(a,b,c)=(a×b)·c
混合积具有下列性质:
1、三个不共面向量a、b、c的混合积的绝对值等于以a、b、c为棱的平行六面体的体积V,并且当a、b、c构成右手系时混合积是正数;当a、b、c构成左手系时,混合积是负数,即(abc)=εV(当a、b、c构成右手系时ε=1;当a、b、c构成左手系时ε=-1)
2、上条性质的推论:三向量a、b、c共面的充要条件是(abc)=0
3、(abc) = (bca) = (cab) = - (bac) = - (cba) = - (acb)
参考资料:搜狗百科——平面向量去百度文库,查看完整内容>
内容来自用户:lyplyp8675480
一、向量有关概念
名称|定义|备注|
向量|既有_______又有_______的量。|向量不能比较大小|
向量的模|向量的大小叫做向量的_______(或_______)|记为_______|若已知,则,模可以比较大小|
零向量|长度为_______的向量,记为_______|零向量与所有向量平行;|与所有向量垂直。|
单位向量|长度等于_______的向量|平行向量|方向_______或_______的非零向量。|与任一向量平行或共线;|直线平行:不包括重合情况|共线向量:包括重合情况|若、都是非零向量,存在实数λ,使|
共线向量|_______向量又叫共线向量。|
相等向量|长度_______且方向_______的向量|特点:1、长度相等;|2、平行且方向一致|
相反向量|长度_______且方向_______的向量|的相反向量是本身|特点:1、长度相等;|2、平行且方向相反|_______|
二、向量的线性运算
向量运算|定义|法则(或几何意义)|备注|
加法|求两个向量和的运算|平行向量与向量平行是不同的!
方向相同或相反的非零向量叫做平行向量。平行是指一种向量之间的相对关系;
而平行向量是指具有平行关系的两个或两个以上的向量。
零向量与任一向量平行。
向量平行的公式如下(转自网上 向量平行的等价条件 -2010年山东省高中教师全员研修)
1、当给定向量以有向线段的形式表示时
向量m与向量n平行m=xn (x为唯一存在的实数,向量n不为零向量).
运用这个结论的时候尤其要注意它需要满足的条件.由此也可引出平面内a,b,c三点共线
向量ab//向量ac//向量bc
对平面内任意一点o有,向量oc=a向量oa+b向量ob(其中满足a+b=1)
a向量oa+b向量ob+c向量oc=零向量(其中满足a+b+c=0)
2、当给定向量以坐标的形式表示时
向量m(m1,m2)与向量n(n1,n2)平行m1*n2—m2*n1=0.
这个推导过程是依据了正交分解(即在直角坐标系下,向量m与向量n的坐标分别为(m1,m2)、(n1,n2)),我们也可以把这个结论推广到一般的向量分解下,即不在直角坐标系下。例如:
已知向量m与向量n,在一组基底{a, b}下的分解式分别m=m3a+m4b、n=n3a+n4n,即可理解为在以向量与向量的基线为坐标轴的坐标系下,向量m与向量n的坐标分别为(m3,m4)、(n3,n4),那么由上面的结论我们可以得到向量m(m3,m4)与向量n(n3,n4)平行m3*n4—m4*n3=0.这个结论我们可以根据“向量m与向量n平行m=xn (x为唯一存在的实数,向量n不为零向量)”得到。
【注】但是要注意的是对于向量垂直的等价条件来说,不能引用到一般情况下。1、对于两个向量a(向量a≠向量0),向量b,当有一个实数λ,使
向量b=λ向量a(记住向量是有方向的)则向量a‖向量b
反之,当向量a‖向量b时,有且只有一个实数λ,能使向量b=λ向量a
2、当向量a=(x1,y1),向量b=(x2,y2)时,
当x1y2=x2y1时,向量a‖向量b,反之也成立选{e1,e2}作为基底,如果
a(x1,y1),b(x2,y2)
则条件a=入b
(x1,y1)=入(x2,y2)=(入x2,入y2)
x1=入x2 (1)y1=入y2(2)
(1)(2)两式的两边分别乘以y2、x2得
x1y2=入x2y2 (3) y1x2=入y2x2(4)
(3)-(4)得x1y2-y1x2=0
当x2,y2不为0时 所以 y1/x1=y2/x2
希望能帮到你哈。。。因为:a//b,则存在λ≠0,使得:
(x1,y1)=λ(x2,y2),则:
x1=λx2且y1=λy2
消去λ,得:
x1/x2=y1/y2
即:x1y2-x2y1=0





